ejemplo:
Una característica de calidad importante en la fabricación de una llanta es la longitud de capa, que para cierto tipo de llanta debe ser de 780 mm con una tolerancia de ±10 mm. La longitud es el resultado de un proceso de corte, por lo que este proceso debe garantizar una longitud entre la especificación inferior EI = 770 y la superior ES = 790, con un valor ideal o nominal de N = 780. Para monitorear el correcto funcionamiento del proceso de corte, cada media hora se toman cinco capas y se miden. De acuerdo con las mediciones realizadas en el último mes, en donde el proceso ha estado trabajando de manera estable, se tiene que la media y la desviación estándar del proceso (poblacional) son μ = 783 y σ = 3, respectivamente. Con base en lo anterior se quiere saber en qué medida el proceso ha estado cumpliendo con especificaciones.
Una primera forma de hacer esto es aplicar lo visto en los capítulos 2 y 3, y grafi car la distribución del proceso. De manera específica, en la fi gura 5.1 se muestra la capacidad del proceso para cumplir con la longitud deseada (suponiendo una distribución normal, con μ = 783 y σ =3), de donde destaca que el proceso no está centrado, ya que la media del proceso, μ = 783, está alejada del centro de las especificaciones. Esta situación causa que aproximadamente 1% de las tiras tenga una longitud superior a lo máximo tolerado (790 mm). Si el proceso se centrara, se lograría cumplir con especificaciones de forma razonable, lo cual significa que la variabilidad del proceso se encuentra en un nivel aceptable. Enseguida se ve cómo los índices de capacidad reflejan las situaciones que se observan.
indice cp (capacidad potencial del proceso)
El índice de capacidad potencial del proceso, Cp, se define de la siguiente manera:
donde σ representa la desviación estándar del proceso, mientras que ES y EI son las especificaciones superior e inferior para la característica de calidad. Como se puede observar, el índice Cp compara el ancho de las especificaciones o la variación tolerada para el proceso con la amplitud de la variación real de éste:
Decimos que 6σ (seis veces la desviación estándar) es la variación real, debido a las propiedades
de la distribución normal (capítulo 3), en donde se afirma que entre μ ± 3σ se encuentra 99.73% de los valores de una variable con distribución normal. Incluso si no hay normalidad, en μ ± 3σ se encuentra un gran porcentaje de la distribución debido a la desigualdad de Chebyshev y a la regla empírica.
Interpretación del índice Cp
Para que el proceso sea considerado potencialmente capaz de cumplir con especificaciones, se requiere que la variación real (natural) siempre sea menor que la variación tolerada. Deaquí que lo deseable es que el índice Cp sea mayor que 1; y si el valor del índice Cp es menor que uno, es una evidencia de que el proceso no cumple con las especificaciones. Para una mayor precisión en la interpretación en la tabla 5.1 se presentan cinco categorías de procesos que dependen del valor del índice Cp, suponiendo que el proceso está centrado. Ahí se ve que el Cp debe ser ma yor que 1.33, o que 1.50 si se quiere tener un proceso bueno; pero debe ser mayor o igual que dos si se quiere tener un proceso de clase mundial (calidad Seis Sigma). Además, en la tabla 5.2 se representó el valor del índice en el porcentaje de artículos que no cumplirían especificaciones, así como en la cantidad de artículos o partes defectuosas por cada millón producido (PPM). Por ejemplo, si el índice Cp = 0.8 y el proceso estuviera centrado, entonces el correspondiente proceso produciría 1.64% de piezas fuera de especificaciones (que corresponde a 16395 partes malas por cada millón producido). Una observación que se deriva de la tabla referida es que el valor del índice Cp no es igual al porcentaje de piezas que cumplen con especificaciones.
Un aspecto que es necesario destacar es que la interpretación que se da en las tablas 5.1 y 5.2 está fundamentada en cuatro supuestos: que la característica de calidad se distribuye de manera normal, que el proceso está centrado y es estable (está en control estadístico), y que se conoce la desviación estándar del proceso. Es decir, la desviación estándar no es una estimación basada en una muestra. La violación de alguno de estos supuestos, sobre todo de los últimos dos, afecta de manera sensible la interpretación de los índices. Más adelante se verá la interpretación de los índices cuando éstos se calculan (estiman) a partir de una muestra.
Si al analizar el proceso se encuentra que su capacidad para cumplir especificaciones es mala, entonces algunas alternativas de actuación son: mejorar el proceso (centrar y reducir variación), su control y el sistema de medición, modificar tolerancias o inspeccionar al 100% los productos. Por el contrario, si hay una capacidad excesiva, ésta se puede aprovechar, por ejemplo: con la venta de la precisión o del método, reasignando productos a máquinas menos precisas, así como al acelerar el proceso y reducir la cantidad de inspección.
En el caso del ejemplo 5.1 de la longitud de capa para las llantas, el índice Cp está dado por:
La variación tolerada es de 20 y la variación real es ligeramente menor ya que es de 18. De acuerdo con la tabla 5.1, el proceso tiene una capacidad potencial parcialmente adecuada y requiere de un control estricto. En función de la tabla 5.2 se espera que si el proceso estuviera centrado arrojaría aproximadamente 0.0967% de las capas fuera de especificaciones, lo cual corresponde a 967 PPM y se considera parcialmente adecuado. Sin embargo, como es claro, a partir de la figura 5.1 el proceso no está centrado (lo que no toma en cuenta el índice Cp), y eso provoca que genere 1.0% fuera de la especificación superior, lo cual corresponde a 10 000 PPM.

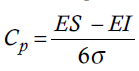




No hay comentarios:
Publicar un comentario